If the natural ggplot2 equivalent to nodes is
geom_point(), then surely the equivalent to edges must be
geom_segment()? Well, sort of, but there’s a bit more to it
than that.

While nodes are the sensible, mature, and predictably geoms, edges are the edgy (sorry), younger cousins that pushes the boundaries. To put it bluntly:
On the ggraph savannah you definitely want to be an edge!
Meet the geom_edge_*() family
While the introduction might feel a bit over-the-top it is entirely
true. An edge is an abstract concept denoting a relationship between two
entities. A straight line is simply just one of many ways this
relationship can be visualised. As we saw when discussing nodes sometimes it is not drawn at all
but impied using containment or position (treemap, circle packing, and
partition layouts), but more often it is shown using a line of some
sort. This use-case is handled by the large family of edge geoms
provided in ggraph. Some of the edges are general while
others are dedicated to specific layouts. Let’s creates some graphs for
illustrative purposes first:
library(ggraph)
library(tidygraph)
library(purrr)
library(rlang)
set_graph_style(plot_margin = margin(1,1,1,1))
hierarchy <- as_tbl_graph(hclust(dist(iris[, 1:4]))) |>
mutate(Class = map_bfs_back_chr(node_is_root(), .f = function(node, path, ...) {
if (leaf[node]) {
as.character(iris$Species[as.integer(label[node])])
} else {
species <- unique(unlist(path$result))
if (length(species) == 1) {
species
} else {
NA_character_
}
}
}))
hairball <- as_tbl_graph(highschool) |>
mutate(
year_pop = map_local(mode = 'in', .f = function(neighborhood, ...) {
neighborhood %E>% pull(year) |> table() |> sort(decreasing = TRUE)
}),
pop_devel = map_chr(year_pop, function(pop) {
if (length(pop) == 0 || length(unique(pop)) == 1) return('unchanged')
switch(names(pop)[which.max(pop)],
'1957' = 'decreased',
'1958' = 'increased')
}),
popularity = map_dbl(year_pop, ~ .[1]) %|% 0
) |>
activate(edges) |>
mutate(year = as.character(year))Link
While you don’t have to use a straight line for edges it is certainly
possible and geom_edge_link() is here to serve your
needs:
ggraph(hairball, layout = 'stress') +
geom_edge_link(aes(colour = year))
There’s really not much more to it — every edge is simply a straight line between the terminal nodes. Moving on…
Fan
Sometimes the graph is not simple, i.e. it has multiple edges between
the same nodes. Using links is a bad choice here because edges will
overlap and the viewer will be unable to discover parallel edges.
geom_edge_fan() got you covered here. If there are no
parallel edges it behaves like geom_edge_link() and draws a
straight line, but if parallel edges exists it will spread them out as
arcs with different curvature. Parallel edges will be sorted by
directionality prior to plotting so edges flowing in the same direction
will be plotted together:
ggraph(hairball, layout = 'stress') +
geom_edge_fan(aes(colour = year))
Parallel
An alternative to geom_edge_fan() is
geom_edge_parallel(). It will draw edges as straight lines
but in the case of multi-edges it will offset each edge a bit so they
run parallel to each other. As with geom_edge_fan() the
edges will be sorted by direction first. The offset is done at draw time
and will thus remain constant even during resizing:
ggraph(hairball, layout = 'stress') +
geom_edge_parallel(aes(colour = year))
Loops
Loops cannot be shown with regular edges as they have no length. A
dedicated geom_edge_loop() exists for these cases:
# let's make some of the student love themselves
loopy_hairball <- hairball |>
bind_edges(tibble::tibble(from = 1:5, to = 1:5, year = rep('1957', 5)))
ggraph(loopy_hairball, layout = 'stress') +
geom_edge_link(aes(colour = year), alpha = 0.25) +
geom_edge_loop(aes(colour = year))
The direction, span, and strength of the loop can all be controlled, but in general loops will add a lot of visual clutter to your plot unless the graph is very simple.
Density
This one is definitely strange, and I’m unsure of it’s usefulness,
but it is here and it deserves an introduction. Consider the case where
it is of interest to see which types of edges dominates certain areas of
the graph. You can colour the edges, but edges can tend to get
overplotted, thus reducing readability. geom_edge_density()
lets you add a shading to your plot based on the density of edges in a
certain area:
ggraph(hairball, layout = 'stress') +
geom_edge_density(aes(fill = year)) +
geom_edge_link(alpha = 0.25)## Warning: The following aesthetics were dropped during statistical transformation: xend
## and yend.
## ℹ This can happen when ggplot fails to infer the correct grouping structure in
## the data.
## ℹ Did you forget to specify a `group` aesthetic or to convert a numerical
## variable into a factor?
Arcs
While some insists that curved edges should be used in standard
“hairball” graph visualisations it really is a poor choice, as
it increases overplotting and decreases interpretability for virtually
no gain (unless complexity is your thing). That doesn’t mean arcs have
no use in graph visualizations. Linear and circular layouts can benefit
greatly from them and geom_edge_arc() is provided precisely
for this scenario:
ggraph(hairball, layout = 'linear') +
geom_edge_arc(aes(colour = year))
Arcs behave differently in circular layouts as they will always bend
towards the center no matter the direction of the edge (the same thing
can be achieved in a linear layout by setting
fold = TRUE).
ggraph(hairball, layout = 'linear', circular = TRUE) +
geom_edge_arc(aes(colour = year)) +
coord_fixed()
Bundling
Edge bundling is a technique to reduce clutter in a network visualization by bundling edges that flows in the same direction. There are various ways of doing this, many with heavy computational cost and the potential to mislead. The technique were initially confined to connections between nodes with a hierarchical structure but has been expanded to general graphs. ggraph provides 3 different bundling geoms with various up- and downsides.
Force directed
This is perhaps the most classic. It treats the edges as an array of points with the propensity to attract each other if edges are parallel. It suffers from bad performance (though the edge bundling geoms uses memoisation to avoid recomputations) and can also be misleading as it doesn’t use the underlying topology of the graph to determine if edges should be bundled, only whether they are parallel.
ggraph(hairball) +
geom_edge_bundle_force(n_cycle = 2, threshold = 0.4)## Using "stress" as default layout
Edge path
An alternative is to let the edges follow the shortest paths rather than attract each other. This means the topology is being used in the bundling and in theory lead to less misleading results. It also has the upside of being faster. The algorithm is iterative so that if an edge has been bundled it is deleted from the graph where the shortest path is being searched in. In this way the edges naturally converge towards a few “highways”.
ggraph(hairball) +
geom_edge_bundle_path()## Using "stress" as default layout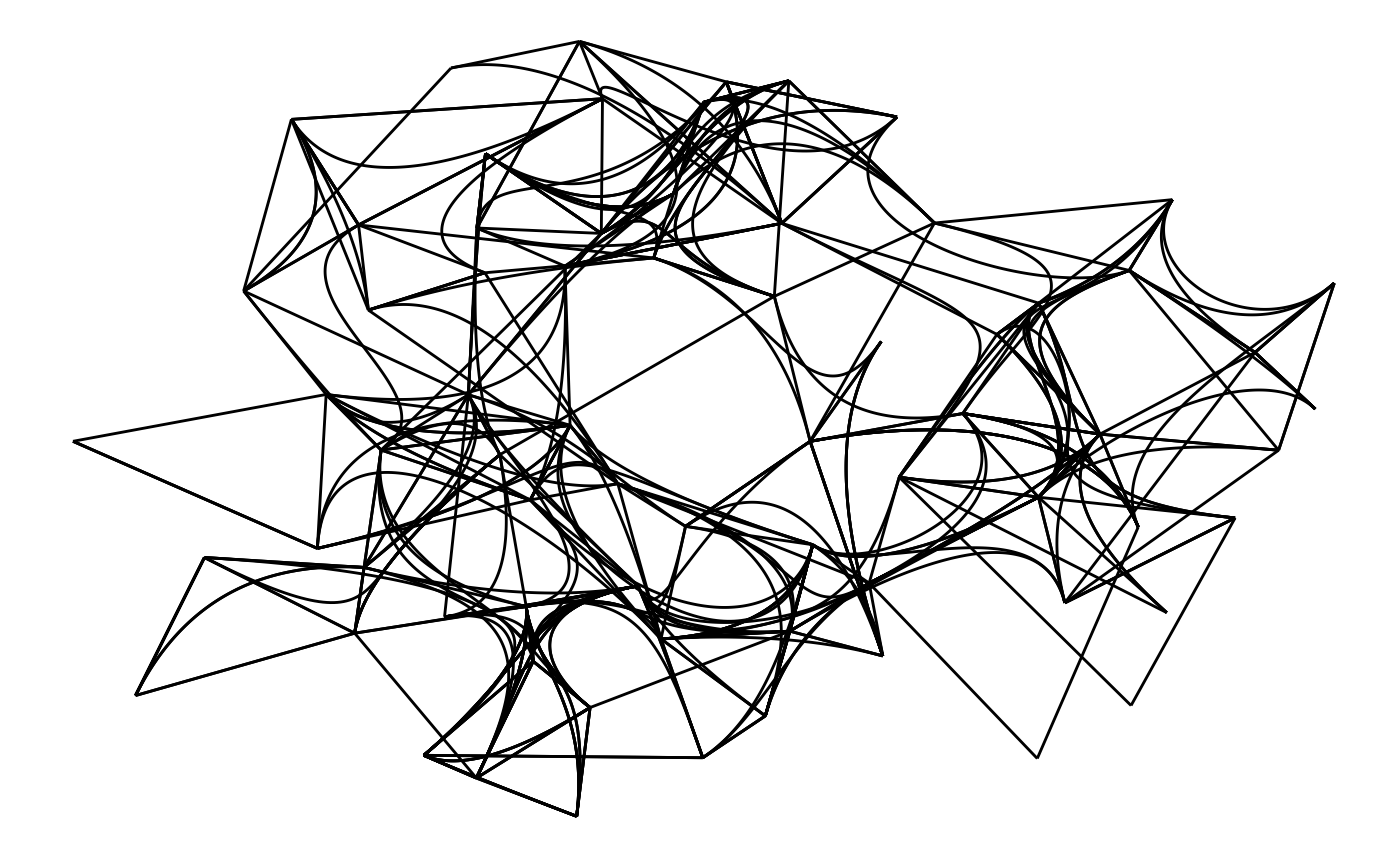
Minimal
In the same vein as edge path bundling but even simpler, you can use the minimal spanning tree of the graph as the scaffold to bundle edges along. As such, it changes to the hierarchical edge bundling approach, just with an implicit hierarchy calculated on the graph. This method is very fast but does create bias in the output as edges will (obviously) travel along the minimal spanning tree thus amplifying that topology.
ggraph(hairball) +
geom_edge_bundle_minimal()## Using "stress" as default layout
Elbow
Aah… The classic dendrogram with its right angle bends. Of course
such visualizations are also supported with the
geom_edge_elbow(). It goes without saying that this type of
edge requires a layout that flows in a defined direction, such as a
tree:
ggraph(hierarchy, layout = 'dendrogram', height = height) +
geom_edge_elbow()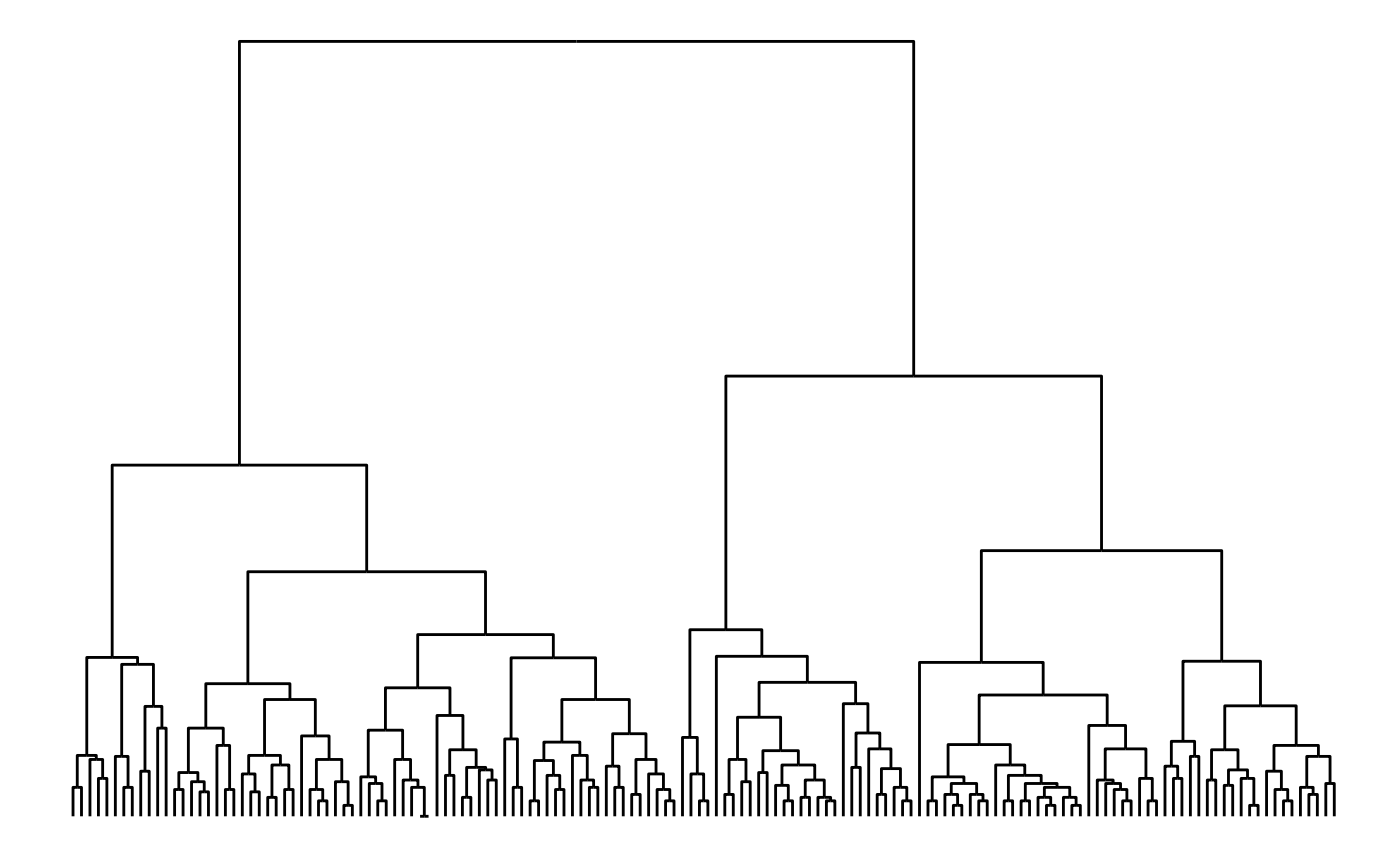
Diagonals
If right angles aren’t really your thing ggraph provides
a smoother version in the form of geom_edge_diagonal().
This edge is a quadratic bezier with control points positioned at the
same x-value as the terminal nodes and halfway in-between the nodes on
the y-axis. The result is more organic than the elbows:
ggraph(hierarchy, layout = 'dendrogram', height = height) +
geom_edge_diagonal()
It tends to look a bit weird with hugely unbalanced trees so use with care…
Bends
An alternative to diagonals are bend edges which are elbow edges with a smoothed corner. It is implemented as a quadratic bezier with control points at the location of the expected elbow corner:
ggraph(hierarchy, layout = 'dendrogram', height = height) +
geom_edge_bend()
Hive
This is certainly a very specific type of edge, intended only for use with hive plots. It draws edges as quadratic beziers with control point positioned perpendicular to the axes of the hive layout:
ggraph(hairball, layout = 'hive', axis = pop_devel, sort.by = popularity) +
geom_edge_hive(aes(colour = year)) +
geom_axis_hive(label = FALSE) +
coord_fixed()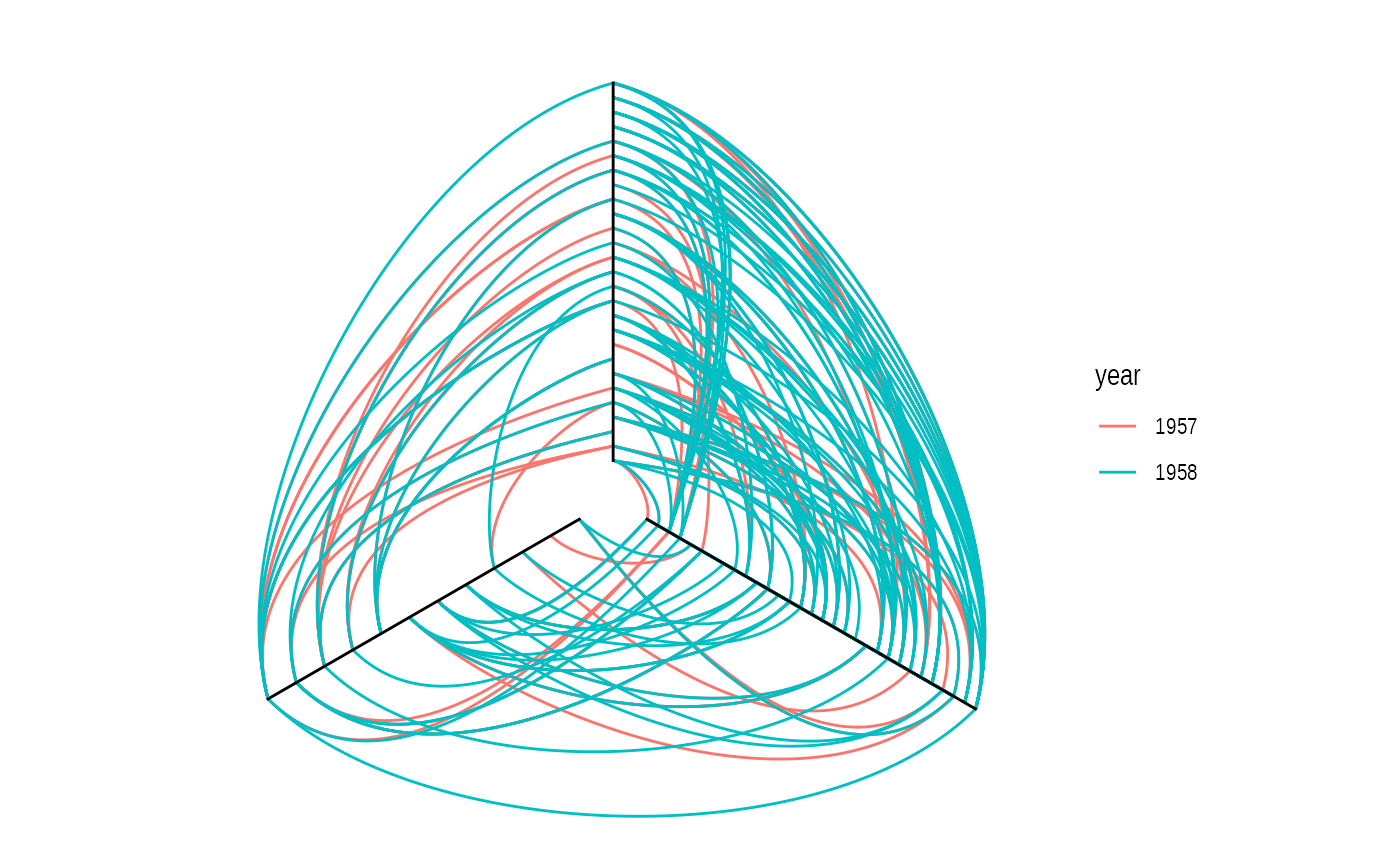
Span
As with the hive edge the geom_edge_span() is made in
particular for a specific layout - the fabric layout. It draws the edge
as a vertical line connecting the horizontal node lines of the layout,
potentially with a terminal shape.
ggraph(hairball, layout = 'fabric', sort.by = node_rank_fabric()) +
geom_node_range(colour = 'grey') +
geom_edge_span(end_shape = 'circle') +
coord_fixed()
Point and tile
It may seem weird to have edge geoms that doesn’t have any span, but the matrix layout calls for exactly that. The terminal nodes of the edge are determined by the vertical and horizontal position of the mark, and for that reason the geom doesn’t need any extend. The point and tile geoms serve the same purpose but are simply different geometry types:
ggraph(hairball, layout = 'matrix', sort.by = bfs_rank()) +
geom_edge_point() +
coord_fixed()
ggraph(hairball, layout = 'matrix', sort.by = bfs_rank()) +
geom_edge_tile() +
coord_fixed()
The three types of edge geoms
Almost all edge geoms comes in three variants. The basic variant (no
suffix) as well as the variant suffixed with 2
(e.g. geom_edge_link2()) calculates a number
(n) of points along the edge and draws it as a path. The
variant suffixed with 0 (e.g. geom_edge_diagonal0()) uses
the build in grid grobs to draw the edges directly (in case of a
diagonal it uses bezierGrob()). It might seem strange to
have so many different implementations of the same geoms but there’s a
reason to the insanity…
Base variant
The basic edge geom is drawn by calculating a number of points along the edge path and draw a line between these. This means that you’re in control of the detail level of curved edges and that all complex calculations happens up front. Generally you will see better performance using the base variant rather than the 0-variant that uses grid grobs, unless you set the number of points to calculate to something huge (50–100 is usually sufficient for a smooth look). Apart from better performance you also get a nice bonus (you actually get several, but only one is discussed here): The possibility of drawing a gradient along the edge. Each calculated point gets an index value between 0 and 1 that specifies how far along the edge it is positioned and this value can be used to e.g. map to an alpha level to show the direction of the edge:
ggraph(hairball, layout = 'linear') +
geom_edge_arc(aes(colour = year, alpha = after_stat(index))) +
scale_edge_alpha('Edge direction', guide = 'edge_direction')
2-variant
Like the base variant the 2-variant calculates points along the edge and draws a path along them. The difference here is that in this variant you can map node attributes to the edge and the aesthetics are then interpolated along the edge. This is easier to show than to explain:
ggraph(hierarchy, layout = 'dendrogram', height = height) +
geom_edge_elbow2(aes(colour = node.Class))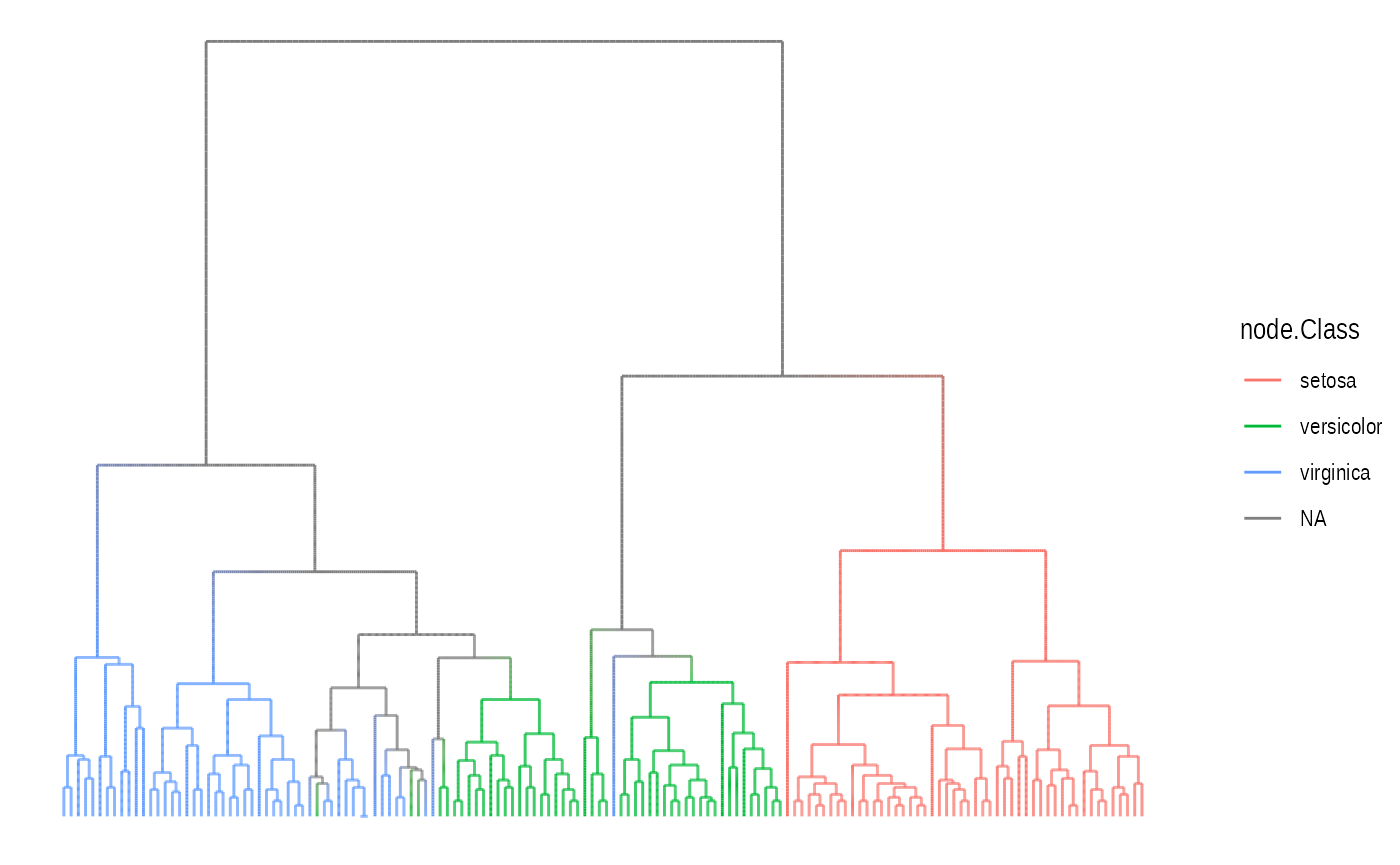
There are considerably more computation going on than in the base variant so unless you need to interpolate values between the terminal nodes you should go with the base variant.
Edge strength
Many of the edge geoms takes a strength argument that denotes their
deviation from a straight line. Setting strength = 0 will
always result in a straight line, while strength = 1 is the
default look. Anything in between can be used to modify the look of the
edge, while values outside that range will probably result in some weird
looks. Some examples are shown below:
small_tree <- create_tree(5, 2)
ggraph(small_tree, 'dendrogram') +
geom_edge_elbow(strength = 0.75)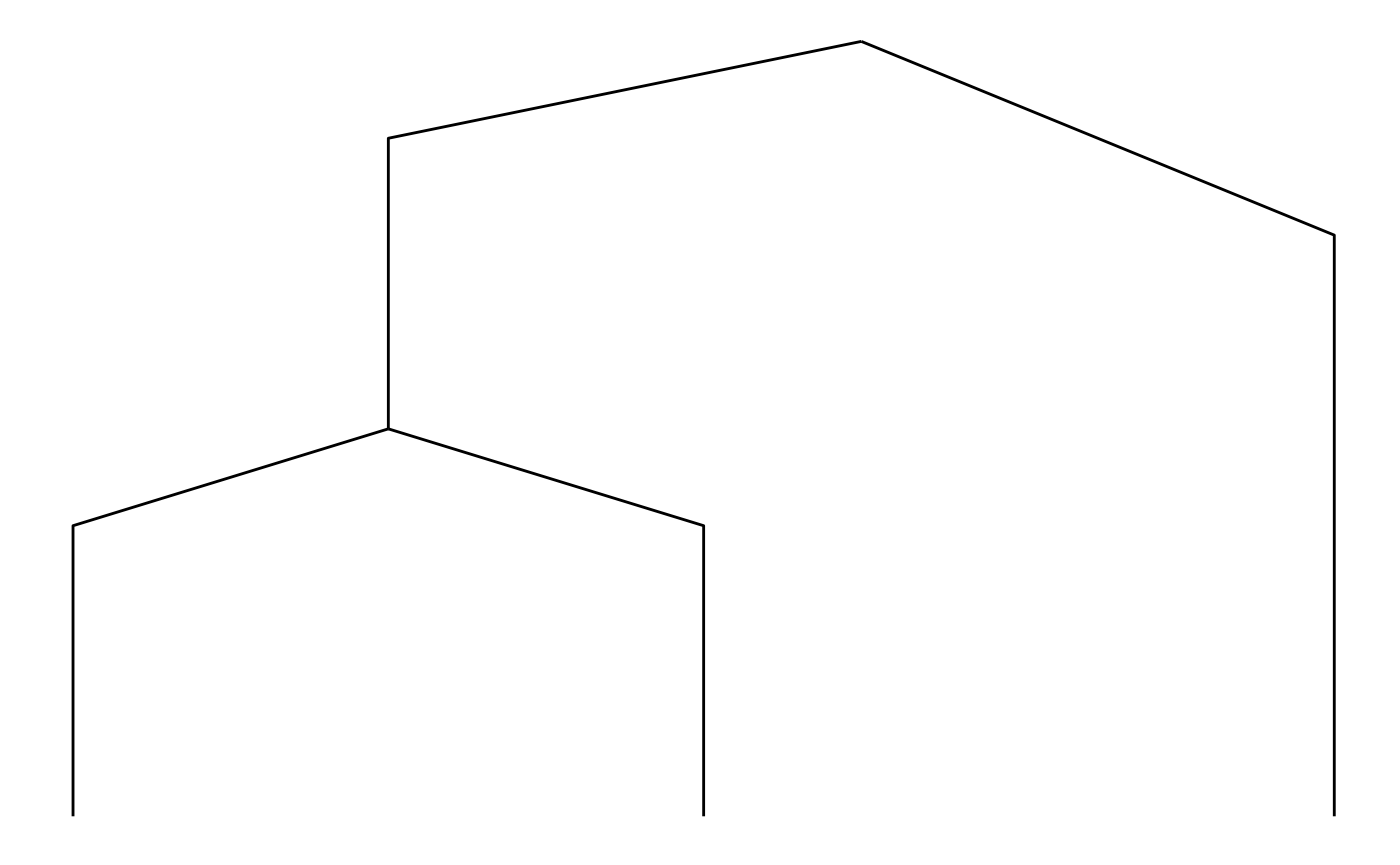
ggraph(small_tree, 'dendrogram') +
geom_edge_diagonal(strength = 0.5)
Decorating edges
An edge is so much more than a line… Well at least it is also potentially an arrow and a label. This section will go into how these can be added. To clearly see the effect here we will use a slightly simpler graph
# Random names - I swear
simple <- create_notable('bull') |>
mutate(name = c('Thomas', 'Bob', 'Hadley', 'Winston', 'Baptiste')) |>
activate(edges) |>
mutate(type = sample(c('friend', 'foe'), 5, TRUE))Arrows
While we saw above that direction can be encoded as a gradient, the
good old arrow is still available. As with the standard
ggplot2 geoms an arrow can be added using the arrow
argument:
ggraph(simple, layout = 'graphopt') +
geom_edge_link(arrow = arrow(length = unit(4, 'mm'))) +
geom_node_point(size = 5)
I hope you think Ugh at the sight of this. The edges
naturally extend to the node center and nodes are thus drawn on top of
the arrow heads. There’s a solution to this in the form of the
start_cap and end_cap aesthetics in the base
and 2-variant edge geoms (sorry 0-variant). This can be used to start
and stop the edge drawing at an absolute distance from the terminal
nodes. Watch this:
ggraph(simple, layout = 'graphopt') +
geom_edge_link(arrow = arrow(length = unit(4, 'mm')),
end_cap = circle(3, 'mm')) +
geom_node_point(size = 5)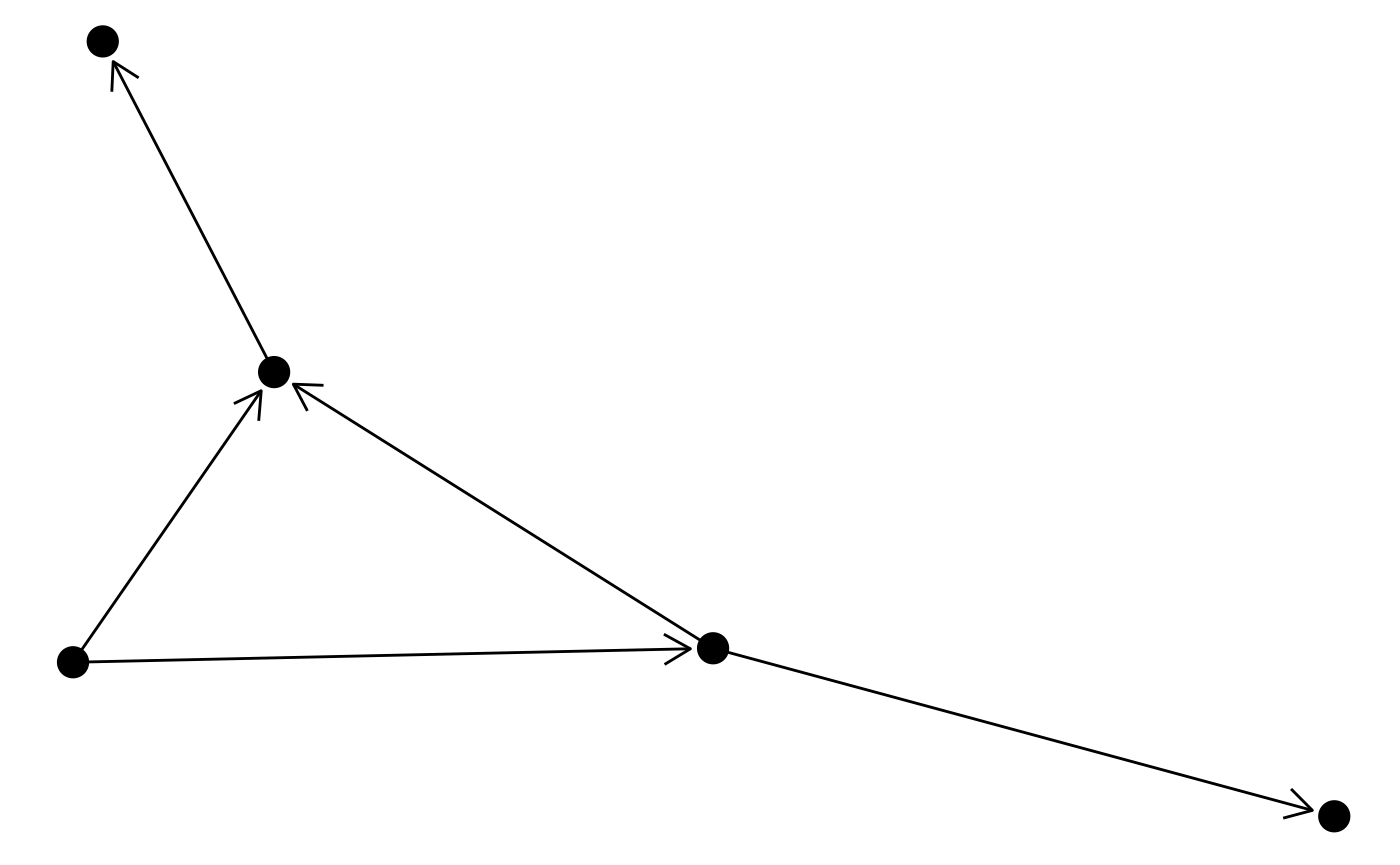
Using the circle(), square(),
ellipsis(), and rectangle() helpers it is
possible to get a lot of control over how edges are capped at either
end. This works for any edge, curved or not:
ggraph(simple, layout = 'linear', circular = TRUE) +
geom_edge_arc(arrow = arrow(length = unit(4, 'mm')),
start_cap = circle(3, 'mm'),
end_cap = circle(3, 'mm')) +
geom_node_point(size = 5) +
coord_fixed()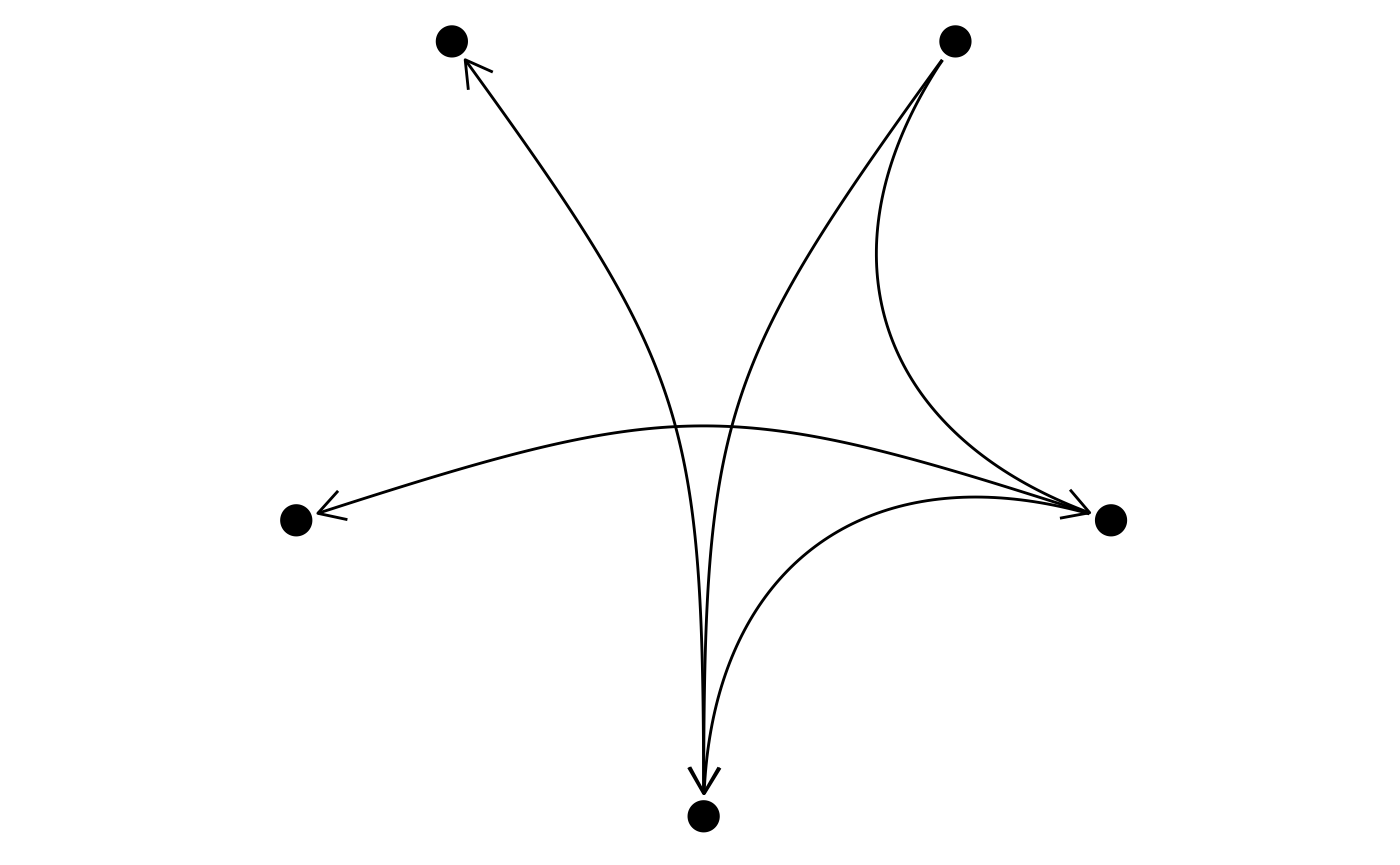
When plotting node labels you often want to avoid that incoming and
outgoing edges overlaps with the labels. ggraph provides a
helper that calculates the bounding rectangle of the labels and cap
edges based on that:
ggraph(simple, layout = 'graphopt') +
geom_edge_link(aes(start_cap = label_rect(node1.name),
end_cap = label_rect(node2.name)),
arrow = arrow(length = unit(4, 'mm'))) +
geom_node_text(aes(label = name))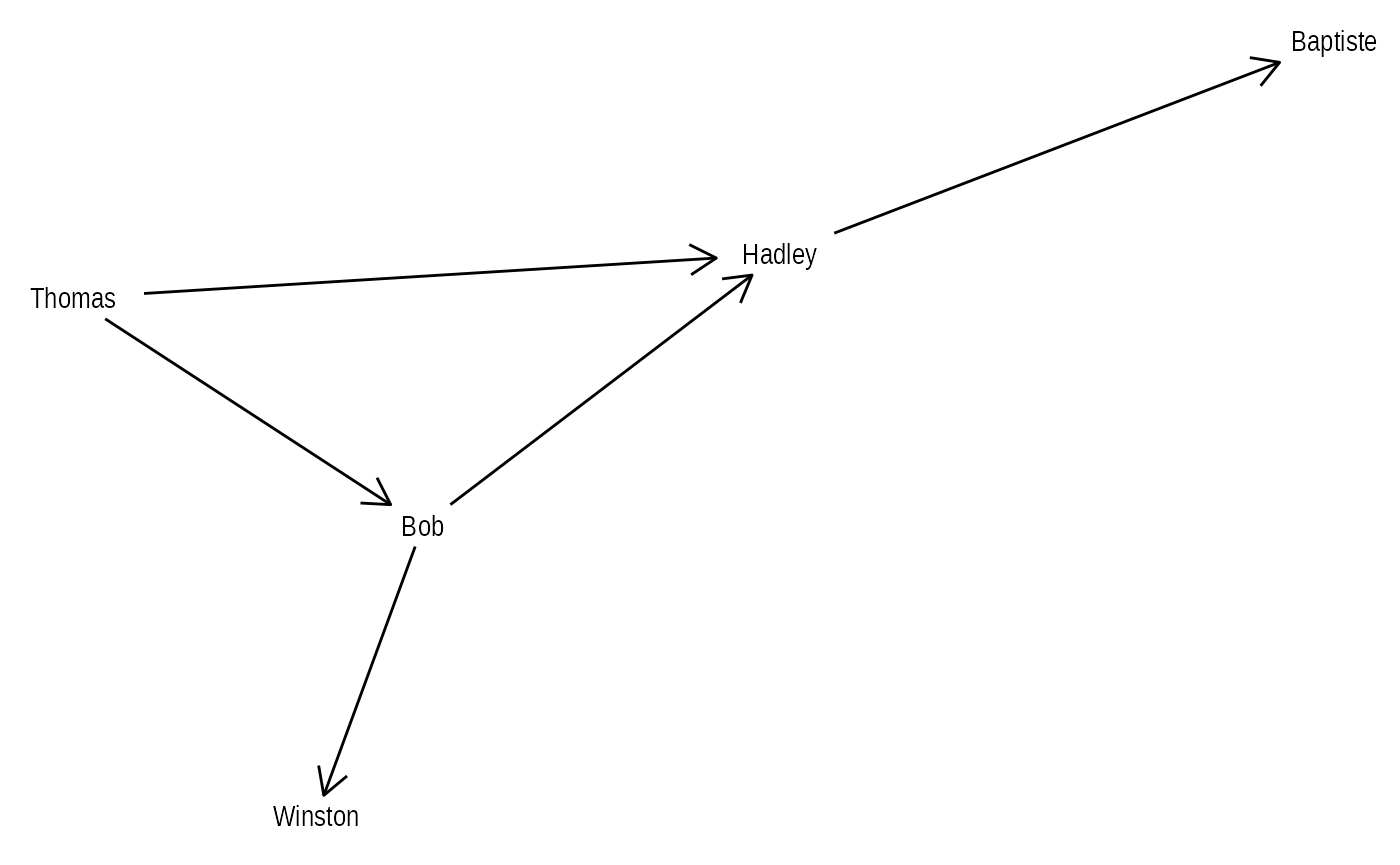
The capping of edges is dynamic and responds to resizing of the plot so the absolute size of the cap areas are maintained at all time.
A quick note on directionality
In ggraph there is no such thing as an undirected graph.
Every edge has a start and an end node. For undirected graphs the start
and end of edges is arbitrary but still exists and it is thus possible
to add arrowheads to undirected graphs as well. This should not be done
of course, but this is the responsibility of the user as
ggraph does not make any checks during rendering.
Labels
You would expect that edge labels would be their own geom(s), but
ggraph departs from the stringent grammar interpretation
here. This is because the label placement is dependent on the choice of
edge. Because of this edge labeling is bundled with each edge geom (but
not the 0-variant) through the label aesthetic
ggraph(simple, layout = 'graphopt') +
geom_edge_link(aes(label = type),
arrow = arrow(length = unit(4, 'mm')),
end_cap = circle(3, 'mm')) +
geom_node_point(size = 5)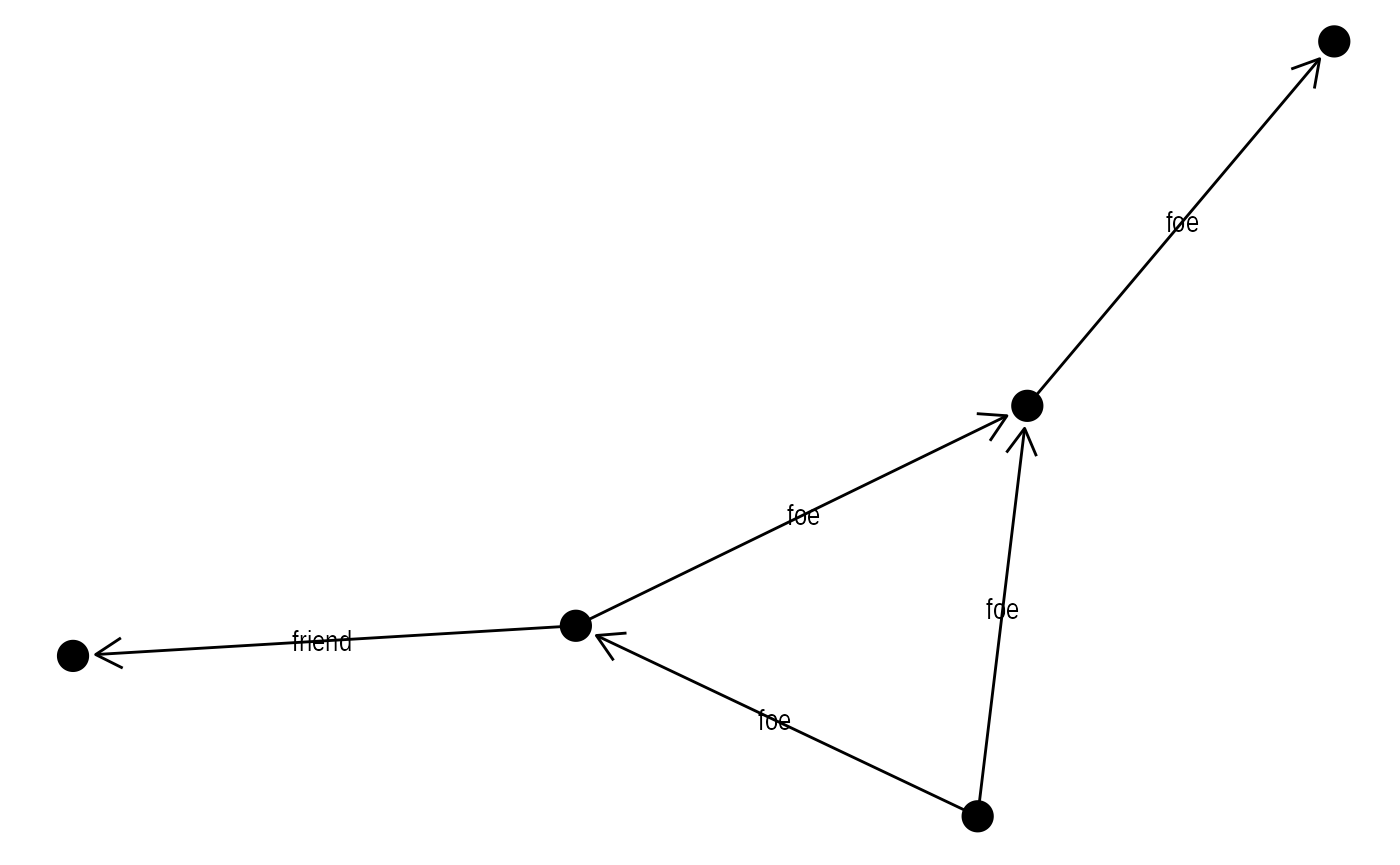
Usually you would like the labels to run along the edges, but
providing a fixed angle will only work at a very specific aspect ratio.
Instead ggraph offers to calculate the correct angle
dynamically so the labels always runs along the edge. Furthermore it can
offset the label by an absolute length:
ggraph(simple, layout = 'graphopt') +
geom_edge_link(aes(label = type),
angle_calc = 'along',
label_dodge = unit(2.5, 'mm'),
arrow = arrow(length = unit(4, 'mm')),
end_cap = circle(3, 'mm')) +
geom_node_point(size = 5)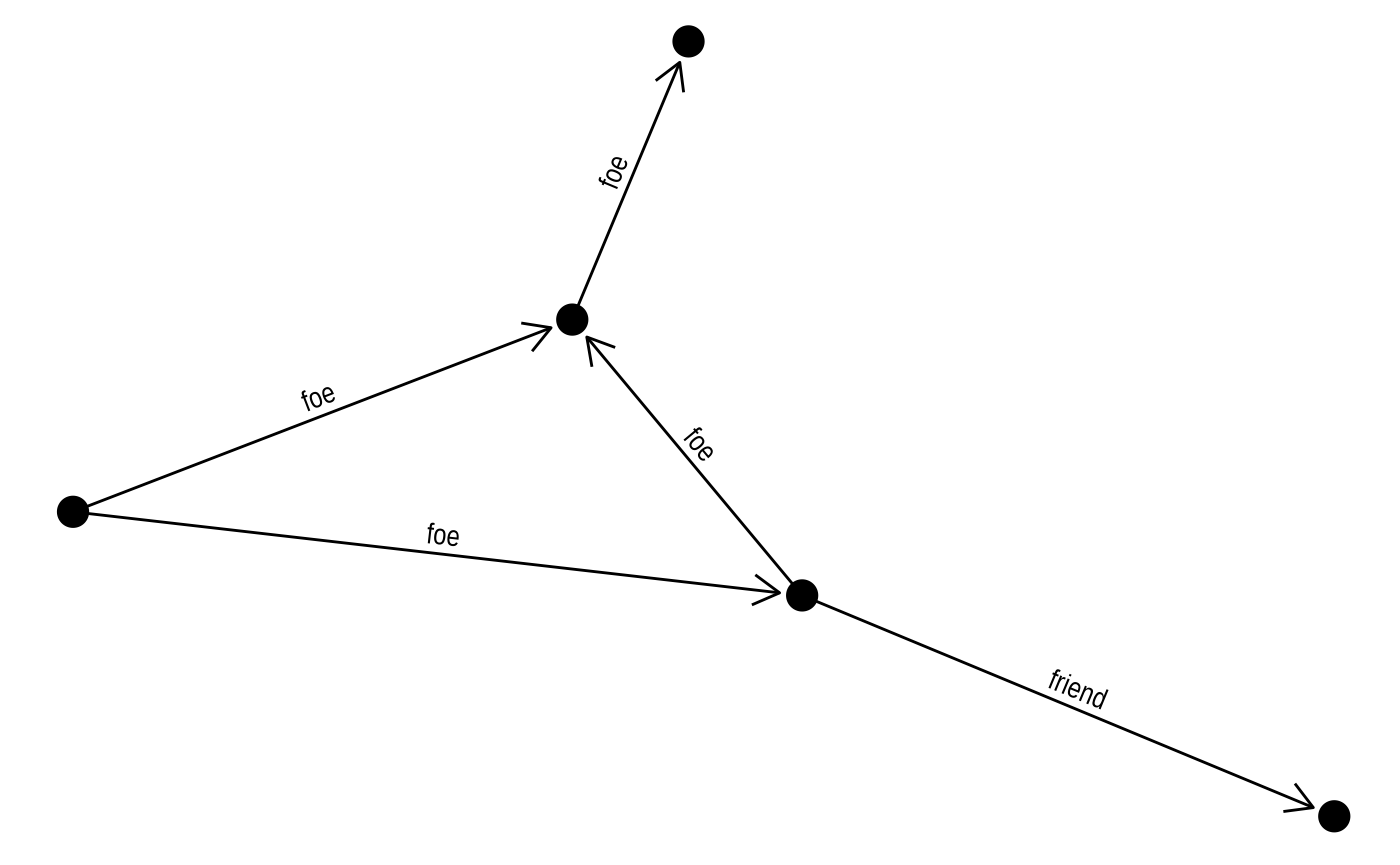
ggraph offers a lot of additional customization of the
edge labels but this shows the main features. As with arrowheads labels
can severely clutter your visualization so it is only advisable on very
simple graphs.
Connections
The estranged cousin of edges are connections. While edges show the
relational nature of the nodes in the graph structure, connections
connect nodes that are not connected in the graph. This is done by
finding the shortest path between the two nodes. Currently the only
connection geom available is geom_conn_bundle() that
implements the hierarchical edge bundling technique:
flaregraph <- tbl_graph(flare$vertices, flare$edges)
from <- match(flare$imports$from, flare$vertices$name)
to <- match(flare$imports$to, flare$vertices$name)
ggraph(flaregraph, layout = 'dendrogram', circular = TRUE) +
geom_conn_bundle(data = get_con(from = from, to = to), alpha = 0.1) +
coord_fixed()
The connection concept is underutilized at the moment but I expect to add more support for this in coming releases.